東大入試問題

「円周の長さ」が「その円の直径」と”比例関係”にあり

その比例定数が円周率となっています。

中1で勉強する、比例の一般式

y＝ax

の

yが円周の長さ（ℓと表します）

aが円周率（πと表します）

xが直径（半径”r”の2倍なので、直径という表現より2rと表現することが多いです）

となり

ℓ＝π×2r

を計算して（数字を文字より前に置く文字式のルールに従って）

ℓ＝2πrとなります。

 

ℓ＝2πr

なので等式変形をすれば

π＝ℓ/2r　（←2r分のℓと読んでください）

円周の長さを直径で割ればよいということです。

しかしそれでは証明は難しそうですし

今回は、円周率である3.14･･････をズバリ出さなくてもよくて

3よりは大きいことを示せばよいので

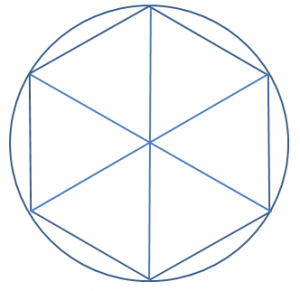
上記のように円に内接する正六角形を想定します

正六角形は上記のように6個の正三角形で出来ています

正三角形の1辺を0.5とします（円の直径は1になります）

そうすると

 

円周は"π"となります

※直径×πなので

1×π＝π

 

正六角形の周りの長さは3となります

※正三角形1辺×６なので

0.5×6＝３

 

円に内接している正六角形なので

正六角形の周りの長さ＜円周の長さ

より

３＜π

となり

円周率は3より大きくなります。

この応用で

円に外接する正六角形で考えると

円周率は3.46よりは小さいことを証明したりできます

（※√3＝1.73とした場合）

さらに内接や外接する円を

正六角形よりも辺の数の多い多角形にすることで

どんどん3.14に近づいていきます

 

埼玉県の入試問題では

公式や定理を利用する問題だけでなく

それが正しいことを証明する問題が出題されることがあります

教科書に出ている公式への理解は、深めておきましょう